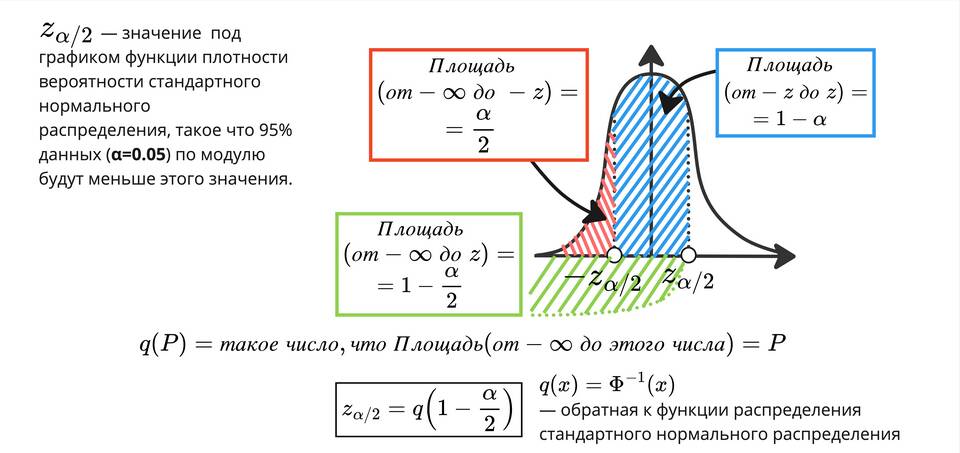
Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит неизвестный параметр генеральной совокупности. Рассмотрим основные формулы для расчета доверительных интервалов.
Содержание
Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит неизвестный параметр генеральной совокупности. Рассмотрим основные формулы для расчета доверительных интервалов.
Основные формулы доверительных интервалов
| Параметр | Формула | Условия применения |
| Среднее значение (σ известна) | X̄ ± Z*(σ/√n) | Нормальное распределение, известное σ |
| Среднее значение (σ неизвестна) | X̄ ± t*(s/√n) | Нормальное распределение, малая выборка |
| Доля | p̂ ± Z*√(p̂(1-p̂)/n | np̂ > 5 и n(1-p̂) > 5 |
| Разность средних | (X̄₁-X̄₂) ± t*√(s₁²/n₁ + s₂²/n₂) | Независимые выборки |
Пошаговый расчет доверительного интервала
1. Для среднего значения (σ известна)
- Вычислите выборочное среднее (X̄)
- Определите уровень доверия (обычно 95%)
- Найдите Z-значение для выбранного уровня
- Рассчитайте стандартную ошибку: σ/√n
- Умножьте Z-значение на стандартную ошибку
- Прибавьте и вычтите полученное значение от X̄
2. Для доли
- Вычислите выборочную долю (p̂)
- Определите уровень доверия
- Найдите соответствующее Z-значение
- Рассчитайте стандартную ошибку: √(p̂(1-p̂)/n
- Умножьте Z-значение на стандартную ошибку
- Получите границы интервала
Критические значения
| Уровень доверия | Z-значение | t-значение (n=30) |
| 90% | 1.645 | 1.697 |
| 95% | 1.960 | 2.042 |
| 99% | 2.576 | 2.750 |
Пример расчета
Для среднего при 95% доверии:
- X̄ = 50, σ = 10, n = 100
- Z = 1.96 (для 95%)
- Стандартная ошибка = 10/√100 = 1
- Погрешность = 1.96 * 1 = 1.96
- Доверительный интервал: 50 ± 1.96 → (48.04, 51.96)
Важные замечания
При малых выборках (n < 30) используйте t-распределение вместо Z-распределения. Для пропорций убедитесь, что выполнены условия np̂ > 5 и n(1-p̂) > 5. При работе с нестандартными распределениями могут потребоваться другие методы расчета.
